Making a homebrew HDTV antenna

Since I work for a TV station now, and we're web-casting a lot of University sports, it behooves me to get more familiar with sports broadcasting, and one of the ways I'm doing that is to watch sports on TV.  Now, I'm still too cheap to pay for cable TV, I'm on my holiday break, and most importantly I haven't built an antenna since my J-pole, so I figured I ought to build myself a TV antenna. 

I'm basing this antenna on plans I found for a UHF bowtie antenna here.  Now, being the sort of guy I am, I can't just blindly follow the recipe. :)  I need to screw around with it a bit, and see if I can improve on the design based on my own particular situation. 

I went to TV Fool's signal locator and put in my address.  It gave me a handy list of all the TV broadcast stations in the area, along with their channel assignments (if you're following along at home, note that you need the actual channel assignment, not the virtual channel.  Sometimes these two things are different).  Next, I consulted Wikipedia for a list of TV channels and associated frequencies.  This told me that all the TV stations in town were in the range of 494 MHz to 698 MHz. 

I think it's safe to assume that the original design is tuned for a broader frequency range than I need.  If I tune the design for my narrower range, maybe I can get another dB or two of gain, which will improve my signal quality.  Also, it's more fun that way. :)

Now for the parts.  I went to the hardware store and bought some deck screws, some washers, and a 2 x 4.  They didn't have any 1 x 3's or 2 x 3's, and I didn't much feel like going somewhere else to see what they had.  I also bought a 75Ω to 300Ω balun, as called for in the design (this design has a 300Ω characteristic impedance).  For the antenna bays, I've got some old wire hangers laying around that need to be put to a good use.  I've also got wire laying around that I can use to interconnect the bays.

In the design, each antenna bay is a pair of 14" wires, folded into a "V" whose ends are 3" apart (so an angle of about 25°).  This is a bowtie antenna, so each side of the bay is a dipole 1/2 wavelength long.  14" gives a wavelength of about 420 MHz, well below the minimum frequency I'm looking for. 

Let me pause a moment to detail how I'm calculating the length of the dipole.  Wavelength (λ) is equal to the speed of light (c) divided by the frequency (f).  So:

λ = c/f

An important thing to note here is that c isn't always c, if you take my meaning.  Generally speaking, if someone mentions c in the context of the speed of light, they mean the speed of light (or other electromagnetic radiation) in a vacuum.  In (e.g.) a metal, however, electromagnetic radiation moves more slowly.  So we introduce a velocity factor, a number that describes just how much slower electromagnetic radiation is going to move in the material than in free space.  If we call the velocity factor v, then we get:

λ = cv/f

This is good.  By introducing the velocity factor into the equation, we can more precisely model how electromagnetic radiation (e.g. radio waves) is going to behave in the wire of the dipole.  But I don't have a velocity factor for steel wire (which is what they make wire hangers out of), so I'm just going to use a value of 1 for v. 

So, back to the antenna, if I want a minimum frequency of 494 MHz, I want to start with a dipole about 12" long.  I can always trim it down later if I need to.

Now, let's get to building!  To start with, I'm going to cut my wire hangers into 8 12" pieces.  And this is tougher than it sounds.  A pair of dikes (diagonal cutters) won't cut it.  Tin snips won't do it.  A stout pair of side-cutters (or "Kleins", electrician's pliers) might do it, but I don't have a pair of those.  What I'm doing instead is taking a big pair of dikes and gripping the wire where I want it to break, then just wiggling the hanger back and forth until it breaks.  Metal fatigue FTW!

8 12" dipoles

As you can see, some of these aren't exactly straight.  A number of wire hangers came from the dry cleaner, and they only have metal on top - the bottom is just thick paper.  So I straightened those as best I could.  I also sanded the center of each dipole because  I'm going to short all the dipoles along each side together at the center.

Dipoles bent so that the distance between each leg is roughly 3"

Here are the bent dipoles.  I've tried to keep the spacing between the two legs to about 3 inches.









Now comes the fun part: drilling the holes and mounting the dipoles.  I got a cordless drill as an early Christmas present; time to put it through its paces!

As per the plans, I drew a line across the board at 2" from one end, then 3 more lines at 5 1/4" intervals (so marks at 2", 7.25", 12.5", and 17.75").  These lines are where the two dipoles in each antenna bay will be placed.




Next, I made two perpendicular marks on each line, 1" apart.  I like things to be even, so I centered the marks, placing them 1.25" from each edge (a 2 x 4 is actually 3.5" wide).  I then drilled pilot holes at each mark for the deck screws.

Here you can see the board with the deck screws already part of the way in.  This makes it easier to place the elements and the connection wire.  I also have two small steel washers on each screw.  The lower holds the dipole element to the board.  The upper will pinch the connection wire between it and the lower washer, providing electrical connectivity.

Next, I added the connection wires between each element. I used insulated wire, and I only stripped those parts of the wire that were going to be in electrical contact with an antenna element.  I've also stripped a place in the center of the antenna to connect the balun.

Here you can see the deck screws where the balun will connect.  Like the other screws, these have washers on them to improve the electrical connection between the wire and the balun.

And this is the antenna with the balun attached.  This is a usable antenna right now, but it's omnidirectional.  Adding a reflector, as recommended in the original plans, will increase the gain of the antenna, but you might want to try this antenna as-is and see how well it works for you. 



I mounted the antenna, sans reflector, in my basement and attached it to my TV.  I'm able to pull in all the stations that TV Fool says are available in my area, including the two analog low-power stations.  But none of those transmitters are more than 30 miles from me, and I don't have any channels from further away.  Once I get the antenna mounted outside, and the reflector attached, I'll report back.

"What news from Plymouth?"

Well, so far as I am aware, Plymouth continues to be in Massachusetts. If this situation should change, I hope one of you, Dear Readers, will be so good as to tell me.

News in my neck of the woods has nothing to do with Plymouth at all. However, if you're stuck on Plymouth, I suggest this brief riveting look at the court of Elizabeth I (Plymouth was an English colony during her reign).

Now, the news of your humble polymath-in-the-making. To begin with, Dear Reader, you might be wondering why the promised posts from NAB never materialized. This is because I did not go to NAB, and I will not be going to the Radio Ink Convergence Conference either. In fact, I have been disqualified altogether from the Technology Apprenticeship Program, and that's because I got a job at KTBG and KMOS, the public broadcasting service of the University of Central Missouri. I'm an engineer! This is a very exciting time for me - so much to learn! Interning at KCUR taught me a bit about radio (though here we have to worry about a thing called "short-spacing" which means we have to have a cardioid antenna pattern - more on that as I learn about it) but I know nothing (yet) about TV.

One of the things I'll be doing at KTBG/KMOS is applying my IT experience and knowledge to our setup in broadcasting. So there will be some software development for various projects in between my regular engineering duties. For example, a short-term project I have is to take the output from KTBG's automation system and feed it into our new Inovonics RDS encoder. The encoder isn't installed yet - maybe John (the chief engineer for KMOS/KTBG) will let me do that too. If this encoder is anything like the unit at KCUR (also an Inovonics) I don't foresee a lot of difficulty; Inovonics uses RS-232 to feed data to the encoder, and the command syntax should be documented in the manual. So it's just a matter of parsing out the data from the automation system and presenting it in the proper format to the RDS encoder. No sweat.

This past Thursday, I made a presentation to the local SBE chapter on IP security. You can view it here, and maybe I'll make a blog post that elaborates on these points a little more.

Today, at the Ararat Hambash, I took the test to upgrade my amateur radio operator's license from General to Extra (I had previously upgraded from Technician to General at the end of March) and passed! This means I now have authorization to operate on all bands and modes available to the Amateur Radio Service (certain bands and modes are reserved for operators with a given license class). Of course, I still don't have any equipment, but that will come in time.

I'm going to the NAB show!

I recently heard about the NAB's Technology Apprenticeship Program. Basically, this is a program for people starting out in broadcast engineering, or people with skills in other technical disciplines - "IT, digital technologies, ... or other related areas", as the website puts it - to get some hands-on experience in the field. Since that's the line of work I'm trying to get into, I applied, and I was accepted! So here's how my next few months are going to go:

April 9 - 14: I'll be flying out to Las Vegas (on NAB's dime, no less) to the NAB show. There are going to be several activities geared specifically for the apprenticeship program participants, (you know what? I'm going to say "apprentices" from now on. "apprenticeship program participants" is a mouthful) and we apprentices will be meeting with leaders in broadcast technology.

May 18 - 19: I'll be flying out to Silicon Valley for the http://www.radioink.com/ Convergence Conference.

June - July: I complete a two month paid internship at a TV or radio station. No idea what station yet.

Finally, in August, I go to DC for a week to work with NAB's Science and Technology Department to develop a presentation to be delivered via webcast at the end of my visit. If I'm permitted, I'll publish a link or something here.

I'm very excited about all of this. Not only is this going to be a really interesting and unique experience, but this is going to be a great start to my broadcast engineering career.

So stay tuned, Dear Reader, for more thrilling tales of broadcast engineering! ;)

Constructing a dummy load

A useful thing to have around is a dummy load. This allows you to tune a new radio (or modifications to an existing radio) without potentially damaging your radio (transmitting without a load connected can damage a transmitter) or causing interference.

Now, I could have bought myself a dummy load for thirty bucks or so. But where's the fun in that? I decided to build one instead, and I found a set of plans for one. Thanks to Ken Kemski, K4EAA for the plans.

To begin with, I went to Westlake Hardware to pick up a 1 qt. paint can and a sheet of aluminum. The original plans recommended brass, but aluminum was cheaper, so I went with that. Little did I know that aluminum is fiendishly difficult to solder with the 60/40 Sn/Pb stuff I have. After I discovered this, I went back to the hardware store and picked up some brass, which turned out to be much nicer to solder.

I then ordered a couple of banana plug posts, 20 3W (Watts)1 k&Omega (1 kΩ = 1000 Ohms); resistors, a 0.01 uF ceramic capacitor, and some BAV21 diodes from Mouser, per K4EAA's part list. For resistors, I went with Vishay metal film resistors. Of the resistors I examined, these had the flattest frequency response curve¹.

So what's the point of all these bits? The can, obviously, is to hold everything. The resistors are to absorb the RF energy and turn it into heat. They'll be submerged in oil (some canola oil that I had laying around) to help dissipate that heat. The brass is to make a couple of plates that hold the resistors. The banana plugs, diodes, and capacitor are all for measuring your transmit power.

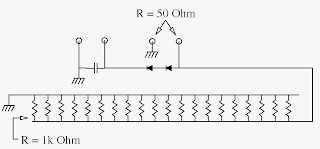
So to begin with, let's look at a schematic of this dummy load.

There are 20 1 kΩ resistors in parallel. This provides a total resistance of 50 Ω. As each resistor is rated for 3W of power, these resistors can safely dissipate 60 W of power without becoming damaged. Submerged in oil, they will be able to dissipate at least 100W, I expect, and probably a bit more.

You'll notice two sets of terminals in the schematic. One set has the capacitor between them, and is connected to one of the plates by two diodes. These terminals are meant for measuring the peak voltage (remember that radio frequency (RF) energy is alternating current (AC), and in AC, the voltage is always changing in both magnitude and direction) the connected transmitter puts out. The diodes ensure that only the positive side of the AC comes to the capacitor, and the capacitor charges up to your peak voltage. You can then determine your transmit power from your peak voltage ².

The other set of terminals is where you connect the transmitter. You can use any connector you like for this - K4EAA uses a BNC; I use an SO-239. Next time I might use a BNC, though.

Now that we've got our schematic squared away, let's build the thing. I started out by making the brass plates that I was going to solder the resistors to. K4EAA (you'll notice a lot of hams will refer to each other by call sign, rather than given name. It's a thing.) cut his out with tin snips. That seems like an excellent idea, but I lack tin snips, and I didn't want to shell out for a pair, so I decided to repeatedly bend the metal back and forth until the metal at the bend fatigued and broke. It's not nearly as elegant, and it's not as pretty, but it works. To make the octagon shape (so that the plates would fit in the paint can) I cut off the corners using diagonal wire cutters.

Next, I divided each plate into twenty sections using a Sharpie, and made an "X" near the edge of each section. I was going for a point that was as far as possible from the center of the plate while maintaining maximum separation from its neighboring points. This was fairly inexact, and I'm sure that if I had taken the time to model this mathematically, I could have found a more optimum resistor spacing. But that level of precision is not really called for here - it's a dummy load, and it's meant to absorb RF. If one resistor gets slightly hotter than its neighbors, the oil is going to go a long way towards mitigating that fact.

Now that I had my "X"'s marked, it was time to start poking holes. I did this with a circular (well, tapered cylinder) needle file I had laying around, and it was pretty easy. Just put some pressure on the file and once it's punctured the metal, rotate it a little bit to widen the hole.

Once the holes were poked, it was time to start attaching resistors. And here I may have made a mistake. Figuring that I wanted the maximum spacing between the plates, to allow for maximum heat dissipation, I only put each resistor through its hole a little bit, i.e., I left long leads on the resistors. I figured that since this was a dummy load, any stray reactance wouldn't matter. I may have incorrect in that assumption, as I'll explain later. At any rate, I soldered all twenty resistors to the bottom plate. To maximize conductivity between the resistor lead and plate, I soldered to both the top and bottom of the plate.

K4EAA recommends, when attaching the top plate, that you cut one resistor lead down to your minimum lead length, then cut the rest progressively longer. That way you can insert the leads a few at a time into the top plate. Still operating under the assumption that I wanted maximum spacing between the plates, and feeling like a bit of a mechanical challenge, I decided against that, and instead managed to get all twenty resistors into the holes. It took quite a bit of fiddling. :) After I got all twenty resistors in, I soldered them to the plate, again top and bottom.

I also needed a hole in the top plate for the back of the SO-239 to go into. My original plan was to push the SO-239 through the hole you see here and attach it via the included mounting nut. This did not prove feasible, however, as the banana plugs got in the way. So instead I widened the hole a bit to maintain a space for the center conductor to go through.

Here you see the hole that the center conductor from the SO-239 will connect to.

I wanted the dummy load to be grounded to the chassis - in this case the paint can. It seemed the simplest way to ensure that both the shield of the SO-239 and the black banana post were at the same ground potential. And when I poked holes (again with the needle file and, in the case of the SO-239, my small wire clippers) in the top of the can, the black banana post had an excellent connection to the can lid. The SO-239, however, didn't have as good of a connection, so I sanded away the coating on the bottom of the lid under the hole for the SO-239. That worked much better. The twisted copper wire you see here attached to the shield of the SO-239 ended up connected to the top brass plate. This ensured both a good mechanical connection from the plates to the can, and also a good electrical connection between the top plate and the can (and thus the shield of the SO-239 and the black banana plug).

You'll notice a piece of insulation under the top left bolt in this picture. That's the red banana plug. Just as the black banana plug had a great electrical connection to the paint can lid, so did the red banana plug. So I widened the mounting hole for the red plug, put some bathroom caulk in it to provide a little lateral stability, then took a piece of insulation from some ladder line I had laying around and attached the red plug to that. This ensured that the red plug was electrically isolated from the can.

Here are the banana plugs and the SO-239 attached to the can lid. The white stuff you see is bathroom caulk. Apart from insulating the red banana plug, it serves to fill in any tiny openings where oil might seep through the lid if the dummy load were to be turned on its side or upside down.

Once the banana plugs and the SO-239 were attached to the can lid, the next step was to connect the SO-239 to the plates. I already mentioned the wire connected to the shield. I also needed a wire connected to the center conductor of the SO-239. I had some scrap ladder line laying around, so I stripped part of the conductor from that to for this purpose.

Once I had everything in place on the lid, it was time to mate the lid assembly and the resistor assembly. I bent the shield wire and attached it to the top plate. I attached the center conductor to the bottom plate and made certain it wasn't going to hit the top plate. I then attached the diodes between the red banana jack and the bottom plate.

Finally, it was time to put the lid on the can. I filled up the can with some canola oil I had laying around (I don't cook with canola any more), gently lowered the resistors into the oil, and tapped the lid shut.

Now it was time to measure the performance of my dummy load.

Having borrowed an MFJ-269 from a friend, it was a simple matter to attach it and measure the SWR for various frequency bands. And up through about 30MHz, it was great - nearly 1:1.  And here's the potential mistake I mentioned earlier: what I really wanted this for was 2 meters - 144 - 148 MHz, and there the SWR wasn't so great - between 1.5 and 2 to 1.

Why, you may, ask, did the SWR change as I increased the frequency? It's not as if I'd put any capacitors or inductors in there, just resistors. But a resistor isn't just a resistor. Let's look at a more accurate schematic for the dummy load:

As I said in footnote 1 (you do read the footnotes, don't you?) an actual resistor has some amount of parasitic reactance due to its physical construction. That reactance is made up of both capacitance (as a resistor has two conductive plates separated by some distance) and inductance (due to Lenz's Law). Those values are relatively small³, but they become significant at higher frequencies.

Basically, I had neglected to account for the effects of reactance for 2 meter frequencies.

So what to do? I could shorten the leads. That would reduce, to some degree, the inductance generated by the resistor leads at the cost of increasing the capacitance between the top and bottom plates (because, again, any two conductive plates have some capacitance between them. This might be a good idea, because capacitive reactance is inversely proportional to applied frequency. When I measured the total impedance with the MFJ-269, I got ~23+10j Ω at 146 MHz, and as I increased the frequency, Xs (the reactive part of the impedance) decreased. That indicates that the primary component of the reactance is capacitive. However, the resistive portion of the impedance was 23 Ω Even if I was able to cut the capacitance to zero, I would still have a resistance of 23 Ω when I want 50.

For now, I'm going to stick with the dummy load the way it is. It won't be perfect for tuning a radio on the 2 meter band, but it will do until I can buy or build something better. And if I get some 10 meter gear, this will be perfect.

Here are a few other approaches to building a dummy load:

• Thread on Worldwide DX with a couple of homebrew dummy loads.  "Captain Kilowatt" in that thread makes an excellent point regarding hot air and a potential need for venting.
• UHF Dummy Load by SV1BSX.  He neutralizes the capacitive reactance in his load with an inductor.
• Saltwater Dummy Load by K5LXP.  I'm not sure how well this would work on 2 meters, though, as the electrodes need to remain under a "significant fraction" of a wavelength, but shorter electrodes are going to get hotter faster.

If you've tried any (or all) of these, let me know!

Footnotes

¹ While an ideal resistor has the same resistance no matter what frequency of AC you put through it, real resistors have some amount of parasitic reactance that varies with applied frequency.

² P = V²/R (Power = Voltage² / Resistance). We can measure peak voltage (less an 0.4 V drop from the diodes) across these terminals. If we take the peak voltage, however, that will give us peak power, when what we really want is average power. So we take the voltage - remembering to add the 0.4V drop back in - divide it by the square root of two to obtain RMS (root-mean-square, or average) voltage, square it, and divide it by 50 Ω to obtain power.

The total inductance in the circuit will be smaller still because the total inductance of a number of inductors in parallel is less than the inductance of any one inductor. However, the total capacitance of a number of capacitors in parallel is the sum of all the individual capacitances.

Constructing a programming interface

A little while ago, I was given a pair of EF Johnson UHF mobile radios. These put out 35 Watts of power, which is nice, but like most radios not specifically designed for amateur use (and several that are, as I understand it) you can't set the operating frequency directly from the radio. Instead, one must use a special programming cable to store a number of frequencies (in this case, about 100, in banks of 16) in the radio. And these cables aren't free - aftermarket versions run about $40 a pop. And as my motto with ham stuff has lately been "why buy a thing when you can build it?", I decided to make one of my own.

There are a couple of schematics out there for this cable, all based around a MAX232 IC (integrated circuit). I used one designed by Kyle Yoksh, K0KN.

Basically, what the MAX232 does is convert RS-232 signal voltage levels to TTL signal levels. So a lot of the work has already been done in the IC. All I had to do was solder the IC to a circuit board, attach some capacitors, attach a female DB9, and attach an appropriate connector to interface with the radio.

I was able to obtain all the necessary parts from Electronics Supply Company here in town. I probably paid a little more than I would have if I'd bought from, say, Mouser Electronics, but I like supporting local businesses.

Soldering the entire circuit together was a bit of a learning experience, which I won't recount here as it's extremely boring in the telling. I know that if I built this circuit again, I'd do it slightly differently, but I'm still pleased with the way I did it.

Remember how I said "appropriate connector" above? This whole "appropriate connector" business is easier said than done. It's an 8-pin connector that looks like an RJ45, but it's more narrow. I wasn't able to find one online, so I decided to adapt a bit of Cat 5 that I had laying around instead. This also had the advantage of not requiring me to find a crimper for that weird connector. So, instead of using the Johnson connector, I'm filing down (sloooowly) the RJ45 on the end of the aforementioned Cat 5 stub. Once I've done that, I just need to secure the board and try it out.

For a project box, I decided to use an old Altoids tin that I had laying around. I drilled a hole in it for the Cat 5 stub, but for the DB9, I ended up poking a hole in it with my needle nose pliers and then just working at it with a metal file and clippers for a while. I made the holes for the screws to secure the DB9 to the box using a sheet metal screw I had laying around. A bit of pressure and it poked right through the tin.

OK, now for some pictures. :)

Here's the project board inside the Altoids tin. As you can see, it's really not that complicated of a circuit - a few capacitors, a voltage regulator, and the appropriate connectors on either side, and that's it.

Close-up of the project board.

And this is what the thing will look like once it's finished.

Kansas City Dilettante is now Kansas City Polymath!

Please update your bookmarks to reference http://kcpolymath.blogspot.com/

Changing my name

It occurs to me that "Kansas City Dilettante" does not exactly convey the impression that I want to convey. I originally chose "Dilettante" to reflect the fact that I was interested in a great many things (despite the fact that most of the blog content, lately, has been about radio in one form or another, I am interested in a great many things). But "dilettante" also conveys someone who only toys with things briefly, then moves on. I'm not that person.

I have often said that when I grew up, I wanted to be Benjamin Franklin. I've always admired Franklin's wide range of skills and knowledge. And a word for someone with a wide range of skills and knowledge, like Franklin, is "polymath", and that's something I aspire to be. So, effective as soon as I can figure out how to make Blogger do it, I'm changing the blog's name to "Kansas City Polymath".

Adventures in J-pole construction

So when I said that the J-pole was soldered together, I neglected to mention that the coax - the thing that I connect my radio to - had not been connected to the antenna.

To begin with, I used a borrowed antenna analyzer (a MFJ-259) to find the point on the antenna where I got the lowest SWR. I then marked those points (there's a point on the 3/4 wave section, and a point on the 1/4 wave stub, and in theory they should be at equal height) on the antenna with a Sharpie. Then I screwed a chassis mount SO-239 connector (photo) into the 1/4 wave matching stub, and added some copper wire wrapped around the base of the connector. This was intended to improve the electrical connection between the 1/4 wave stub and the side of the connector that connects to the shield of the coax. I'm not sure it was strictly necessary, though. :)

I had previously soldered a piece of solid core copper wire that I had laying around to the center conductor of the SO-239. After I got the connector screwed into the 1/4 wave stub, I tried soldering the end of the wire to the 3/4 wave section of the antenna at the low SWR point I had previously marked. My soldering iron wouldn't get the copper pipe hot enough for the solder to stick - not surprising, since copper is an excellent conductor of heat - so I ended up using the blowtorch I had used to solder the antenna together to begin with. This worked much better, and when all was said and done, I had an SWR of between 1.1 and 1.2 at 146 MHz.

Today I covered the wire and everything but the threads on the SO-239 with electrical tape to protect them from the elements, and to make sure that nothing could short the matching stub and the 3/4 wave section (apart from the bottom of the "J"). I then (with my upstairs neighbor's permisssion) attached a couple of U-bolts to the railing of the back staircase. They will hold the mast that the j-pole is mounted on to the railing. I might fabricate another mast out of something or other later to get some additional height - I haven't decided yet. I didn't connect any feed line to it, as I don't have a UHF -> F adapter.

Soon, I will have a working outdoor antenna!

The J-pole is soldered together!

Tonight I soldered together the J-pole I mentioned in my last post.

Conditions were less than ideal for this. Not having a garage, and it being awfully cold outside, I had to work in a basement. On the plus side, the basement was relatively warm. On the minus side, it was awfully dirty down there. I kept things as clean as I could, though.

Another less than ideal thing was the flux I used. I purchased a kit from the hardware store that came with a small roll of solder and a small tube of flux. The tube of flux had a thick plastic lid, and I didn't have anything to puncture it with, so I ended up heating up a piece of scrap copper wire and using that to puncture the tube. I only managed this once, however, so the flux came out in a thin ribbon.

But, all problems and less than ideal conditions aside, the j-pole is together! Now all I need to do is find the 75 Ohm match point and I'll be good to go. Now, experienced hams might have noticed that I said 75 Ohms in my last sentence and be a bit confused. After all, most ham equipment is designed for 50 Ohm loads, and you generally want the best impedance match you can get, so as to maximize your power output. But as it happens, I have a bunch of leftover 75 Ohm RG6 that various cable installers have left with me, and I don't want it to go to waste. So I'm going to try and use that as feedline, and try and set something up to match that impedance as best I can. It was suggested in this thread on QRZ that if I make sure my 75 Ohm line is a multiple of 1/2 a wavelength, I can then connect a bit of 50 Ohm line at the radio end. We'll see how that goes. :)

Adventures in ham radio

In my quest to become a broadcast engineer and general polymath, I've started getting into ham radio.¹. I got my Technician-class license in August of last year, and started operating on EchoLink, which provides VoIP connections to other ham operators and those repeaters connected to EchoLink. I made a couple of "Slim Jim"-type antennas, one out of twin-lead, the other out of ladder-line, but didn't actually get a radio until fairly recently.

My current radios are a Midland 13-505 that I bought at the last hamfest, and a pair of EF Johnson 9800 series radios that were given to me by a fellow ham. The Midland radio operates on the 2 meter band, which covers (for hams) 144 - 148 MHz. The Johnson radios operate on the 70 cm band, 420 - 450 MHz.

Neither of these radios is exactly ideal. The Midland is locked (unless I can find or build a synthesizer) to those frequencies for which it has crystals installed. As the Midland dates to the early 1970s, crystals to fit it are fairly rare. The Johnson covers the entire 70 cm band, but requires a special programming cable which I do not currently possess. I have, however, found two sets of plans on the Internet for building such a cable (here and here), so I think that I shall soon have that problem sorted.

As of yet, I have not been able to make a QSL (a contact) with either radio. Several times I have heard traffic on the Midland radio, but I have yet to be heard. I have heard nothing on the Johnson. I'm hoping all that will change soon, though, as I'm building a new antenna. It's another J-Pole (note that the "Slim Jim" is a special case of the J-Pole), but this time, I'm making it out of 1/2" copper tubing.

I used plans by G.E. "Buck" Rogers, K4ABT to get the proper lengths of copper tubing. I went to Westlake Hardware in Westport to buy the tubing, caps, tee, and elbow, and they were kind enough to cut the pipe in the lengths I needed at no charge. I haven't assembled it yet, as I don't know how to solder copper pipe together, but once I have, I plan to mount it on the railing to the stairs at the back of my house. That will give me a reasonable amount of height, especially compared to where I have my antenna now - hanging on the wall above a window in the rear of my house.

That's all for now, Dear Readers. I'll keep you posted (sporadically, of course) on my further adventures in ham radio. And I've still got all manner of things to talk about at KCUR. :)

¹Before you ask, Dear Reader, no, I still haven't learned where the "ham" in "ham radio" comes from. I'm sure it's on the Internet somewhere.